Sixteen Phoenix Magic Diamonds

[emmanuelg]

Sixteen Phoenixes

 

This is a continuation of the series of discussions on Geomantic Figures

inserted into 4X4 Magic Squares. Previously, I took one of the three

4X4 Pan-Magic, “Magic Carpet” Magic squares, and inserted Geomantic

figures into it. Rotating the square onto one corner, it becomes a diamond.

After connecting the matched pairs of the Geomantic figures with

differently-colored ribbons, it forms a symmetrical pattern that resembles

a phoenix rising from a fire.

 

 

 

I have provided links for the images in this document in large and small format, in case























anyone wants to





 

print them.


https://emmanuelg.dreamwidth.org/file/35121.png single diamond with numbers

https://emmanuelg.dreamwidth.org/file/35006.png Single phoenix with ribbons

 

The Significance of “Magic Carpet” Squares

 

Magic Squares sometimes have the ‘Magic Carpet’ property. If you generate

the same Magic Square over and over again horizontally and vertically to

make a carpet of 4x4 Magic Squares, you can select any 4X4 region of the

Magic Carpet and get a Pan-Magic Magic Square.

 

 

https://emmanuelg.dreamwidth.org/file/38824.png – large

https://emmanuelg.dreamwidth.org/file/36654.png --small

https://emmanuelg.dreamwidth.org/file/37299.png --small

https://emmanuelg.dreamwidth.org/file/37456.png --small with internal borders

 

An Aside--The Magic Toroid

 

It is possible to roll a 4X4 Pan Magic Square into a cylinder. Joining the

opposite ends of the Square into a cylinder has the same effect as creating

a row of Magic Squares.

It is also possible to bend the cylinder into the shape of a toroid (a ring, or donut).

This joins the top and bottom of the Pan Magic Square – A Magic Toroid.

Here’s a link to another blog with more information about these toroids;

 

https://carresmagiques.blogspot.com/2020/04/from-magic-square-to-magic-torus.html

 

 

The Magic Toroid has all the properties of a Magic Carpet Magic Square in a

very compact form. I have not evaluated it with respect to Geomancy–Will

probably have to make one sometime, and I don’t have a good idea of how

to do that. Possibly a ring with 4 cylindrical sections, each of which have

4 numbers? They would have to be able to be rolled from the inside to the

outside of the toroid while keeping the same relationship to each other.

Possibly a set of springs on the inside would do this, similar to the construction

of the Rubik’s Cube? I will have to think about it…

 

The Sixteen Phoenixes

 

As pointed out above, if you shift the 4X4 frame by one row, you get a different

variation of the magic square that has all the properties of the original. Shift the

frame 2 rows, yet another magic square. Shift 3 rows and you get a fourth

variation. But if you shift the frame 4 rows, you get the original magic square again.

 

What if we shift the frame by columns? We get a similar result–Three

additional variations, then back to the original.

 

What if we shift the frame by one row, then shift that one, one column

at a time? Again, there are three more variations generated, then back t

o the single-row frame shift again.

 

When we continue this until all possible frame-shift and row-shift

possibilities have been tried, we end up with sixteen variations of

the Pan-Magic Square.

 

It would be possible to have the full set of sixteen Magic Diamonds

in a piece of the Magic Carpet as small as 7X7. However, it is also

a little difficult to compare and contrast the different variations of the

Pan Magic Square if we leave them in this compact form. We can

see all of them at one time by drawing a 4X4 frame around the Square

in the upper right corner of the Magic Carpet. Then we skip a column

and draw another 4X4 frame. We can do the same thing vertically by

skipping a row at the bottom of the original frame, and framing the next

4X4 square. When we have framed four squares horizontally and four

squares vertically under them, we will have framed the sixteen

4X4 variations of the Magic Square.

 

What happens if we turn this Magic Carpet onto its point to make a

Magic Diamond, and insert the Geomantic Figures in place of the

numbers? Will the variations of the original Phoenix Diamond

Magic Square have different patterns if we draw the lines between matched pairs?

 

We seem to get sixteen Magic Phoenixes, grouped in four groups of four.

Within each group, One Phoenix points up, one to the left, one to the right,

and one points downward. The array of sixteen Phoenixes has multiple

concatenating symmetries within the groups of four, and between

different groups of four. It has the look and feel of a mathematical visual fugue.

 

https://emmanuelg.dreamwidth.org/file/36899.png Diamond Carpet Ribbon Small

https://emmanuelg.dreamwidth.org/file/37922.png Diamond Carpet Ribbon Large

 

 

I printed out this carpet-diamond on a piece of 11 x 17-inch paper to get an

overview of it. The more I look at it, the more I see. For example, in the

top group of 4 diamonds, all the Phoenix heads are Populus. All the Fire

hearts are Via. The Phoenix Hearts are (one each) Fortuna Minor, Acquisitio,

Fortuna Major, Amissio. The Phoenix Hearts in all four groups of 4 are always

Fortuna Minor, Acquisitio, Fortuna Major, and Amissio. The Phoenix Heads

within each group of 4 always match–But only the completely symmetrical

figures appear as phoenix heads– 4 Populus heads, 4 Via, 4 Conjunctio,

and 4 Carcer. The symmetries and parallel structures go on and on.

 

Significance for Geomancy

 

What is the significance of sixteen types of Geomantic Magic Diamonds?

Well at this point, I don’t really know. I had just gotten a feel for mapping

a Geomantic Reading into just one Geomantic Magic Diamond. How

would I figure out which of the sixteen Geomantic Diamonds to use for a

given reading? It is tempting to assign a Geomantic Figure to each of the

sixteen Geomantic Diamonds in the set–But what would be the basis for

that? I am not saying that there is no significance or that it is unknowable,

only that I do not (yet) know the significance or how to make use of it, at

least at this point.

 

Groups of Four

 

One other interesting observation: The Phoenixes are drawn by linking

matched pairs of Geomantic Figures with lines. When we draw the lines,

they connect three Geomantic Figures together. As previously noted, in

the original Geomantic Phoenix Diamond, four of these lines of three form

a Querent-Judge-Quesited triplet, and four do not.

 

The Magic Carpet Magic Squares are composed of patterns of four

Geomantic Figures that repeat on each horizontal, vertical, and diagonal line.

For this reason, when we look at the Phoenix Diamond Magic Carpet,

we see that each line of three linked figures has a fourth figure off of

each end of it. In this way, each group of three is actually a group of four.

 

Since the Phoenix pattern is composed of 8 ribbons that connect the matching

pairs of Geomantic Figures, you would think that there are eight groups of four–

However, one group is the group that forms the spine of the Phoenix and the

vertical line through the fire. These two groups of three are actually the same

group of four in two iterations, so there are actually seven unique groups of

four figures that are involved in the Phoenix Diamond pattern. Of course,

there are a lot more possible groups of 4 in a set of sixteen items; Might be

4 factorial x 16/2. I will have to look that up–But there are just 7 groups of

four that are affiliated with the Phoenix Diamond pattern.

 

Further, all of the groups of 4 contain a set of two of the symmetrical figures.

Either the groups contain Populus and Via, or they contain Conjunctio and Carcer.

 

We can arrange them in a hexagonal group of seven, like the holes in a Ritz Cracker.

 

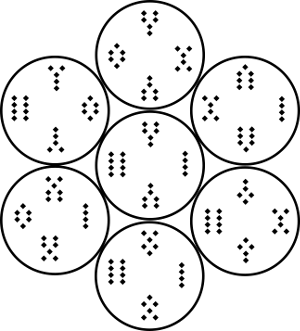
https://emmanuelg.dreamwidth.org/file/34282.png Seven4s- Large

https://emmanuelg.dreamwidth.org/file/35966.png Seven4s Small

 

As an aid to comprehension, we can draw a blue arc next to sets of three

that form a valid Querent-Judge-Quesited group, and a red arc next to sets

of three that would form a valid Querent-Judge-Quesited group if the

Judge in the Middle were its complementary figure instead.

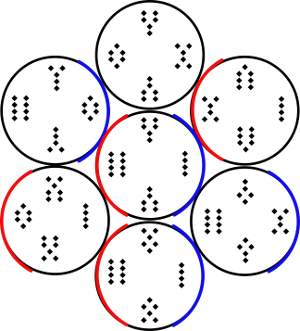
https://emmanuelg.dreamwidth.org/file/35653.png Seven4sPosNeg—Small

https://emmanuelg.dreamwidth.org/file/34485.png Seven4sPosNeg Large

 

When we do this, we find that there is one group of four with a positive and

a negative arc; one group with neither positive nor negative arc; and balancing

and related groups with either a positive or a negative arc. Graphically it makes sense.

 

What is the significance for Geomancy? Completely unknown at this point.

 

We can also insert the ribbons that connect paired Geomantic Figures

into this diagram, and see what happens:

 

https://emmanuelg.dreamwidth.org/file/35379.png Seven4sRibbon Small

https://emmanuelg.dreamwidth.org/file/34602.png Seven4sRibbon Large

 

Again, remarkable symmetries. Note that some of the Geomantic figures appear

only once. Some appear 2 times, 3 times, or 4 times. Again, there are symmetries

in the frequencies of appearance of the figures:

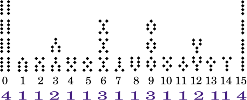
https://emmanuelg.dreamwidth.org/file/36131.png Frequency Large

https://emmanuelg.dreamwidth.org/file/36480.png Frequency Small

 

Summary

 

There may be more than a lifetime of investigation here. Since a person has to

start somewhere, I plan to try some of the other 15 Phoenix Diamonds for Geomantic

Castings. And Geomancy itself is likely to provide direction for explorations.

 

If you have access to a color printer, I’d recommend printing out the 16-Phoenix

diamond magic carpet, and the 7-circle diagram. They are very interesting.