emmanuelg

Sixteen Phoenixes

This is a continuation of the series of discussions on Geomantic Figures

inserted into 4X4 Magic Squares. Previously, I took one of the three

4X4 Pan-Magic, “Magic Carpet” Magic squares, and inserted Geomantic

figures into it. Rotating the square onto one corner, it becomes a diamond.

After connecting the matched pairs of the Geomantic figures with

differently-colored ribbons, it forms a symmetrical pattern that resembles

a phoenix rising from a fire.

I have provided links for the images in this document in large and small format, in case

anyone wants to

print them.

https://emmanuelg.dreamwidth.org/file/35121.png single diamond with numbers

https://emmanuelg.dreamwidth.org/file/35006.png Single phoenix with ribbons

The Significance of “Magic Carpet” Squares

Magic Squares sometimes have the ‘Magic Carpet’ property. If you generate

the same Magic Square over and over again horizontally and vertically to

make a carpet of 4x4 Magic Squares, you can select any 4X4 region of the

Magic Carpet and get a Pan-Magic Magic Square.

https://emmanuelg.dreamwidth.org/file/38824.png – large

https://emmanuelg.dreamwidth.org/file/36654.png --small

https://emmanuelg.dreamwidth.org/file/37299.png --small

https://emmanuelg.dreamwidth.org/file/37456.png --small with internal borders

An Aside--The Magic Toroid

It is possible to roll a 4X4 Pan Magic Square into a cylinder. Joining the

opposite ends of the Square into a cylinder has the same effect as creating

a row of Magic Squares.

It is also possible to bend the cylinder into the shape of a toroid (a ring, or donut).

This joins the top and bottom of the Pan Magic Square – A Magic Toroid.

Here’s a link to another blog with more information about these toroids;

https://carresmagiques.blogspot.com/2020/04/from-magic-square-to-magic-torus.html

The Magic Toroid has all the properties of a Magic Carpet Magic Square in a

very compact form. I have not evaluated it with respect to Geomancy–Will

probably have to make one sometime, and I don’t have a good idea of how

to do that. Possibly a ring with 4 cylindrical sections, each of which have

4 numbers? They would have to be able to be rolled from the inside to the

outside of the toroid while keeping the same relationship to each other.

Possibly a set of springs on the inside would do this, similar to the construction

of the Rubik’s Cube? I will have to think about it…

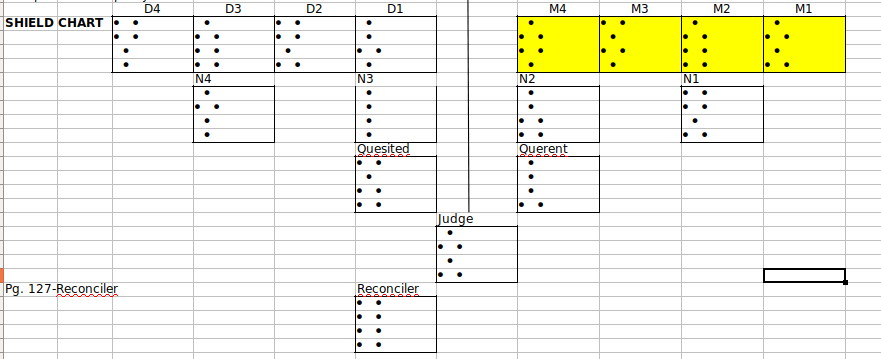
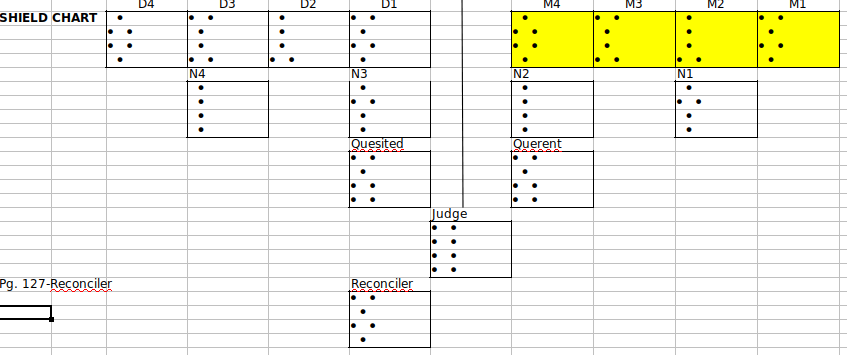
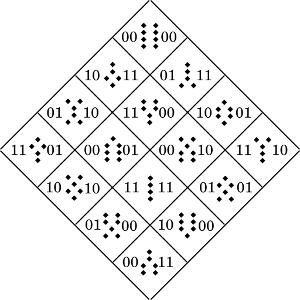
The Sixteen Phoenixes

As pointed out above, if you shift the 4X4 frame by one row, you get a different

variation of the magic square that has all the properties of the original. Shift the

frame 2 rows, yet another magic square. Shift 3 rows and you get a fourth

variation. But if you shift the frame 4 rows, you get the original magic square again.

What if we shift the frame by columns? We get a similar result–Three

additional variations, then back to the original.

What if we shift the frame by one row, then shift that one, one column

at a time? Again, there are three more variations generated, then back t

o the single-row frame shift again.

When we continue this until all possible frame-shift and row-shift

possibilities have been tried, we end up with sixteen variations of

the Pan-Magic Square.

It would be possible to have the full set of sixteen Magic Diamonds

in a piece of the Magic Carpet as small as 7X7. However, it is also

a little difficult to compare and contrast the different variations of the

Pan Magic Square if we leave them in this compact form. We can

see all of them at one time by drawing a 4X4 frame around the Square

in the upper right corner of the Magic Carpet. Then we skip a column

and draw another 4X4 frame. We can do the same thing vertically by

skipping a row at the bottom of the original frame, and framing the next

4X4 square. When we have framed four squares horizontally and four

squares vertically under them, we will have framed the sixteen

4X4 variations of the Magic Square.

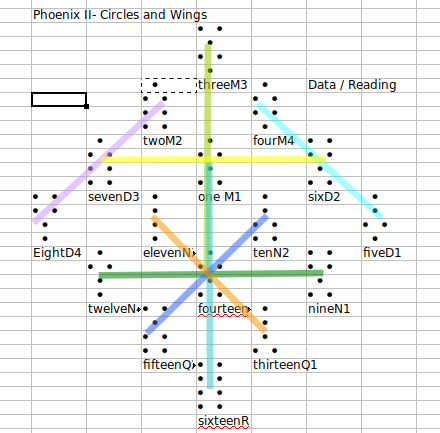
What happens if we turn this Magic Carpet onto its point to make a

Magic Diamond, and insert the Geomantic Figures in place of the

numbers? Will the variations of the original Phoenix Diamond

Magic Square have different patterns if we draw the lines between matched pairs?

We seem to get sixteen Magic Phoenixes, grouped in four groups of four.

Within each group, One Phoenix points up, one to the left, one to the right,

and one points downward. The array of sixteen Phoenixes has multiple

concatenating symmetries within the groups of four, and between

different groups of four. It has the look and feel of a mathematical visual fugue.

https://emmanuelg.dreamwidth.org/file/36899.png Diamond Carpet Ribbon Small

https://emmanuelg.dreamwidth.org/file/37922.png Diamond Carpet Ribbon Large

I printed out this carpet-diamond on a piece of 11 x 17-inch paper to get an

overview of it. The more I look at it, the more I see. For example, in the

top group of 4 diamonds, all the Phoenix heads are Populus. All the Fire

hearts are Via. The Phoenix Hearts are (one each) Fortuna Minor, Acquisitio,

Fortuna Major, Amissio. The Phoenix Hearts in all four groups of 4 are always

Fortuna Minor, Acquisitio, Fortuna Major, and Amissio. The Phoenix Heads

within each group of 4 always match–But only the completely symmetrical

figures appear as phoenix heads– 4 Populus heads, 4 Via, 4 Conjunctio,

and 4 Carcer. The symmetries and parallel structures go on and on.

Significance for Geomancy

What is the significance of sixteen types of Geomantic Magic Diamonds?

Well at this point, I don’t really know. I had just gotten a feel for mapping

a Geomantic Reading into just one Geomantic Magic Diamond. How

would I figure out which of the sixteen Geomantic Diamonds to use for a

given reading? It is tempting to assign a Geomantic Figure to each of the

sixteen Geomantic Diamonds in the set–But what would be the basis for

that? I am not saying that there is no significance or that it is unknowable,

only that I do not (yet) know the significance or how to make use of it, at

least at this point.

Groups of Four

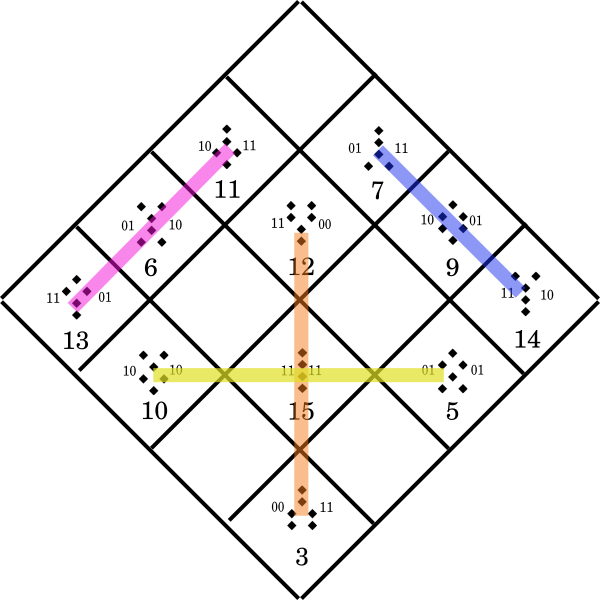
One other interesting observation: The Phoenixes are drawn by linking

matched pairs of Geomantic Figures with lines. When we draw the lines,

they connect three Geomantic Figures together. As previously noted, in

the original Geomantic Phoenix Diamond, four of these lines of three form

a Querent-Judge-Quesited triplet, and four do not.

The Magic Carpet Magic Squares are composed of patterns of four

Geomantic Figures that repeat on each horizontal, vertical, and diagonal line.

For this reason, when we look at the Phoenix Diamond Magic Carpet,

we see that each line of three linked figures has a fourth figure off of

each end of it. In this way, each group of three is actually a group of four.

Since the Phoenix pattern is composed of 8 ribbons that connect the matching

pairs of Geomantic Figures, you would think that there are eight groups of four–

However, one group is the group that forms the spine of the Phoenix and the

vertical line through the fire. These two groups of three are actually the same

group of four in two iterations, so there are actually seven unique groups of

four figures that are involved in the Phoenix Diamond pattern. Of course,

there are a lot more possible groups of 4 in a set of sixteen items; Might be

4 factorial x 16/2. I will have to look that up–But there are just 7 groups of

four that are affiliated with the Phoenix Diamond pattern.

Further, all of the groups of 4 contain a set of two of the symmetrical figures.

Either the groups contain Populus and Via, or they contain Conjunctio and Carcer.

We can arrange them in a hexagonal group of seven, like the holes in a Ritz Cracker.

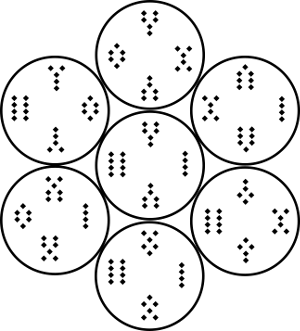
https://emmanuelg.dreamwidth.org/file/34282.png Seven4s- Large

https://emmanuelg.dreamwidth.org/file/35966.png Seven4s Small

As an aid to comprehension, we can draw a blue arc next to sets of three

that form a valid Querent-Judge-Quesited group, and a red arc next to sets

of three that would form a valid Querent-Judge-Quesited group if the

Judge in the Middle were its complementary figure instead.

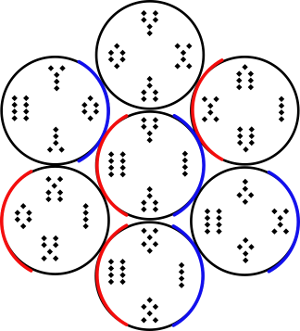
https://emmanuelg.dreamwidth.org/file/35653.png Seven4sPosNeg—Small

https://emmanuelg.dreamwidth.org/file/34485.png Seven4sPosNeg Large

When we do this, we find that there is one group of four with a positive and

a negative arc; one group with neither positive nor negative arc; and balancing

and related groups with either a positive or a negative arc. Graphically it makes sense.

What is the significance for Geomancy? Completely unknown at this point.

We can also insert the ribbons that connect paired Geomantic Figures

into this diagram, and see what happens:

https://emmanuelg.dreamwidth.org/file/35379.png Seven4sRibbon Small

https://emmanuelg.dreamwidth.org/file/34602.png Seven4sRibbon Large

Again, remarkable symmetries. Note that some of the Geomantic figures appear

only once. Some appear 2 times, 3 times, or 4 times. Again, there are symmetries

in the frequencies of appearance of the figures:

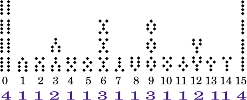
https://emmanuelg.dreamwidth.org/file/36131.png Frequency Large

https://emmanuelg.dreamwidth.org/file/36480.png Frequency Small

Summary

There may be more than a lifetime of investigation here. Since a person has to

start somewhere, I plan to try some of the other 15 Phoenix Diamonds for Geomantic

Castings. And Geomancy itself is likely to provide direction for explorations.

If you have access to a color printer, I’d recommend printing out the 16-Phoenix

diamond magic carpet, and the 7-circle diagram. They are very interesting.

Geomantic Magic Diamonds

Introduction

To understand this article, you will need to be familiar with the concepts of Geomancy. It would also be helpful to have a grasp of Magic Squares.

If you are interested in Geomancy, I recommend “The Art and Practice of Geomancy by John M. Greer. Here’s a link:
https://www.amazon.ca/Art-Practice-Geomancy-Divination-Renaissance/dp/1578634318/ref=sr_1_1?keywords=john+greer+geomancy&qid=1587006509&sr=8-1

If you would like to know more about Magic Squares, I recommend these websites;

Grogono’s Magic Squares
https://www.grogono.com/magic/index.php

Cafe 64 Net – 4X4 Magic Squares
http://www.cafe64.net/numbers/4x4/4x4.html

There is a lot of detail available about Magic Squares, and even some information about using them with Geomantic figures. My goal is to summarize a way to put the two together and hopefully to provide a way to use them for divination. This is very much a project in development, and I am nowhere near a complete understanding of this topic. For those that may be interested, it is a place to start.

Developing the Geomantic Diamond

Magic Squares are typically a square arrangement of numbers in which all the rows, all the columns and the diagonals add up to the same number. They can be any size, but we will look at the 4X4 Magic Squares, each of which contains the sixteen numbers from 0 to 15.

Geomancy uses sixteen characters. Each of these can also be thought of as a binary number from 0 to 15. What would happen if we replace the numbers in a Magic Square with the Geomantic figure that shares its numeric value?

We will look at one Magic Square for this article, number 0105 from the Cafe64.net website (above). This is an example of a ‘Pan-Magic’ square or ‘Magic Carpet’ square;

Every row adds to 30. Every column adds to 30. Both diagonals add to 30. The 4 corners add to 30. Any group of 2X2 squares adds to 30, and the 4 corners of any 3X3 square within the 4X4 square also add to 30. There are 880 possible 4X4 Magic Squares—They all have at least some of these characteristics, and cafe64.net provides a picture of each one of them!
For our purposes, we are going to rotate this square 1/8 turn (45 degrees) so that it becomes a Magic Diamond. We are also going to add a picture of a geomantic figure to each box as well as the 4-digit binary number for each box;

This diagram is kind of busy! To help us take it in, what if we choose a colored path to connect each of the paired Geomantic figures within it? There are eight paired Geomantic Figures, so here is a list of them along with a colored path to represent them:

We can draw paths on the Geomantic Diamond to link the paired figures:

Phoenix Diamond 0105 with Paths

After some meditation on this picture, it seems to me to represent a Phoenix rising out of a fire;
Here is the fire;

And the Phoenix;

Here are the paths depicting the Phoenix rising from the fire, without the numbers and Geomantic Figures.

Note that the paths all overlap, to some extent. Some paths are only touched by the end of another path. Others have a segment of overlap, and others cross entirely over another path. Because of their connections, it is possible to find a path from any box to any other box, traveling along the paths. Notice also that each single colored pathway crosses over three boxes.

We can think of these as paths in space. Perhaps we can apply Geomancy to them! Returning the figures to the diagram, we can apply Geomantic thinking to this Magic Diamond and see where it takes us;

The three characters in each path can be thought of as a spectrum linking the two geomantic figures on each end. The character in the center of each path is typically the endpoint of another path. Its likely that the pathways drawn on the other 879 4X4 Geomantic Diamonds will often display different characters. Maybe topics for the future...

Notice also that some boxes have more connections than others.
Box 12 (Fortuna Major) is connected to three ribbons. It is also in the center of the Phoenix, so let’s call this node the Heart of the Phoenix.
Box 15 (Via) is connected to five ribbons. Since it is in the center of the Fire, we can call this node the Heart of the Fire.
Box 6 and Box 9, the Wings of the Phoenix, have two path connections each. We can call their connection points ‘nodes.’
These 4 nodes, which connect all the paths, are themselves arranged symmetrically within the Geomantic Magic Diamond.
We can look at a list of the 8 paths, which resemble the Querent – Judge – Quesited Triplicates in Geomancy. Perhaps unlike them, it’s not clear which end is the Querent, and which end is the Quesited! It may be more useful to think of each of them as a continuum. We can pay attention to the figure in the middle that holds the place of Judge;

From top to bottom above;

Grey: Change – Stability Judge = Fortuna Major Phoenix heart

Brown: Sorrow – Joy Judge = Via Fire heart

Red: Passion – Wisdom Judge = Via Fire heart

Orange: Fort Minor – Fort Major Judge = Via Fire heart

Yellow: Loss – Gain Judge = Via Fire heart

Green: Isolation – Cooperation Judge = Fortuna Major Phoenix heart

Blue: Beginnings – Endings Judge = Carcer Phoenix Right Wing

Purple: Man – Woman Judge = Conjuctio Phoenix Left Wing

The Heart of the Fire (Via) Judges five of these paths, and the Heart of the Phoenix Judges three of them. The wings each have their own Judge.

What story does this Geomantic Diamond tell us? It seems to me a bit like the story of a life.

The Phoenix rises from the fire, so we start with the fire first.
Starting with the Vertial axis, A journey from Fortuna Minor to Fortuna Major. Going Counterclockwise, a pathway from sorrow to joy. Then going right to left, a path from loss to gain. Then diagonally from passion to wisdom. All of us travel back and forth on these axes throughout life.

Ascending to the Phoenix Fortuna Major is the pathway from change to stability. Right wing, beginnings link to endings via Carcer – We all have a beginning and an ending, and we’re locked into it! Fortuna Major bridges Isolation to Cooperation; Cooperation links Puer to Puella, speaking of a relationship.
Fire seems to describe the experiences of building a life and maturing, and the Phoenix describes building a relationship. Again, the paths could be traveled in both directions. The direction might be different from one reading to the next.

Paths in Space

Perhaps we can look at these paths as ‘paths in space.’ We could take an individual Geomantic reading and put its figures along the paths, much in the same way that we put a geomantic reading into the House Diagram. A geomantic reading, including the Reconciler is a set of 16 characters. It’s just a matter of figuring out where to put the characters in the Geomantic Diamond.

Geomantic Principles

Figures generate other figures. Directions go Right to Left, Top to Bottom. End links to Beginning (as in the case of the Reconciler, and the House Chart). Analysis is in 3’s. --These principles are some of the basic ways of looking at a Geomantic Reading. Perhaps we can use them for placement.

The Shield Chart is generated from Right to Left, and Top to Bottom. Starting at the top, we put the 4 Mothers (M1 to M4) in the top four boxes. M1 goes in the Heart of the Phoenix, and M2, M3, and M4 are placed clockwise in the other 3 boxes. Daughter 1, and 2 (D1 and D2) are placed in the Right Wing, and D3 and D4 are placed in the Left Wing. The Nieces are placed under the Daughters. Daughter and Niece Placement generally follows a counterclockwise, Right-to-Left direction. The last four figures are placed in the bottom four boxes—Querent (Q1) , Judge (J) and Quesited (Q2) are placed counterclockwise in pretty much the same position as you find them in the Shield Chart. The Reconciler R is the final figure generated, and it goes in the bottom box of the diamond. This placement puts Judge (J) at the Heart of the Fire. This placement puts M1 and J above R, and M1 and J are used to generate R.

Why this placement, and not another one? I am really not sure. I tried a number of other placement patterns, and this one seems to work better than the other ones. Combining the motions of the 4 Mothers and the Querent-Judge-Quesited-Reconciler seems to trace a figure-8 or infinity sigil. The overall placement of Geomantic Characters is about the same as the Shield Chart, and the symmetry makes me happy. It just feels right to me. Perhaps there is a better placement pattern out there somewhere!

Geomantic Readings

It might be good to try some examples:

1)
15 April 2020 – How will today go?

The Shield chart casting (Left side, above) is inserted onto the pathways of the Phoenix Diamond (right side).

The hearts of the Fire and Phoenix are Amissio/Loss. The right wing node Albus/Wisdom on the lifespan
path and the left wing node Laetitia/Joy on the relationship path seem very positive.

Treating each path of three characters as a querent-judge-quesited triplet, we can follow the rising of the phoenix upward from the fire.

Fire Paths:

Orange; Populus-Amissio-Amissio. Many moving into loss. Note that Populus and Amissio combined make Amissio. This triplet path has an internal judge. Many/most triplets on the pathways do not form a Querent-Judge-Quesited triplet—But this one does. Pathway is Fortuna minor/major axis, so this may address financial losses.

Brown; Cauda Draconis-Amissio-Via. At the end of loss, a journey. External Judge=Tristitia (from Cauda Draconis + Via)
Pathway is Sorrow/Joy, so possibly an ending or new love and a journey.

Yellow: Albus-Amissio-Puella. Wisdom in loss goes to love. External Judge = Carcer (from Albus + Puella).
Pathway is Loss-Acquisition. Loss will happen, possibly financial, but it will turn out for the best. Note that Amissio appears in the yellow path of the Phoenix Diamond, but not same position.

Red; Fortuna Minor-Amissio-Rubeus. Quick loss with treachery/passion. External Judge = Laetitia (from Fort Minor + Rubeus).
Pathway is Wisdom-Passion. Note that Rubeus appears on the Wisdom-Passion Path in the Phoenix Diamond, but not in the same position.

Phoenix Paths:
Grey: Amissio-Amissio-Acquisitio. Many losses, then a gain. External Judge = Via (from Amissio + Acquisitio).
Path is Change/Stability. Large losses go to gain in stability. Note that Rubeus is in the same path and placement as in the Phoenix Diamond.

Blue: Puer-Albus-Carcer. Boldness>Wisdom>Stability/Isolation. External Judge = Rubeus.
Path is Beginnings/Endings (Lifetime) , so Boldness is called for, but wisest to be in isolation. Carcer is on the blue path in the Phoenix Magic Diamond, but not in same position.

Green: Albus-Amissio-Laetitia. Wisdom in Loss goes to Joy. Note Wisdom and Loss parallel placement in the Yellow path. Note-Internal Judge.
Path is Isolation/Cooperation. With the Yellow path, Cooperation is the wisest way through loss.

Purple: Laetitia-Laetitia-Fortuna Major. Much joy goes to fortune. External Judge = Puella.
Path is Man/Woman (Relationship). Joy and gain in relationship.

Results:

Losses:
On the 15th I realized that my work hours have been cut back from 40 hours per week to 29 hours per week, due to COVID.
My head tech quit to go to a better-paying job with better benefits. That could be what the Brown path was about, but I knew it was likely before the reading.

Fire Paths;
These paths seem to tell about issues in the background that I already knew about.

Phoenix Paths;
These seem to be concerned with my personal life. Isolation the right choice for us, although it means lost income. Result is a better relationship with my spouse. We went shopping for a while that day, then stayed home. The home time was better.

2) Should I Study Geomantic Magic Diamonds?

Charts:

In advance of casting the reading, I began with the intent to read the answer from the Geomantic Diamond chart—This because it is better to choose what diagram you read from; reading from more than one diagram for the same casting often gives conflicting results.

That said, this unusual shield chart has daughters identical to the mothers. This means that the horizontal rows of dots adds up the same as the vertical figures. So in a way, the 4 mothers are a sort of 4X4 Magic Square in and of themselves.
Its not a standard interpretation, but Rubeus in Querent and Quesited confirms to me, in this case, not to look at the Shield Chart for this one. On to the Phoenix Diagram, shown with the Phoenix Magic Diamond 0105;

Fire Heart: Populus
Phoenix Heart: Acquisitio
Right Wing Node: Cauda Draconis
Left Wing Node: Conjunctio

These seem to say ‘Yes’ for the most part. Cauda Drac is possibly the exception.

Fire Paths:

Orange: Acquisitio-Populus-Acquisitio. Very great gain (together?). Internal Judge.
Path = Fortuna Minor/Major.

Brown: Rubeus-Populus-Puella. Hmmm, Drama/Intrigue, lots of it, ending in love(?) External Judge=Via complements Populus and matches Phoenix Diamond.
Path = Sorrow/Joy-- A lot of intense emotion on this path.

Yellow: Puella-Populus-Via. In love, many take the long road. External Judge = Rubeus.
Path = Loss/Acquisition.

Red: Via-Populus-Rubeus. Long way for many to/with drama/passion(?). External Judge = Puella. This path + external judges are very similar to Yellow
Path = Passion/Wisdom. Via and Rubeus occupy Red in the Phoenix Diamond, but in different positions.

Phoenix Paths:

Grey: Populus-Acquisitio-Conjunctio. Much gained working together. External Judge =Conjunctio. Conjunctio is on the Grey Path in Phoenix Diamond, but not same position.
Path = Change/Stability.

Blue: Acquisitio-Cauda Draconis-Carcer. Gain Ends in Prison? The end of gains is stability/isolation? External Judge=Fortuna Minor. Carcer and Cauda Drac are both in the same section in Phoenix Diamond, but positions switched.
Path = Beginnings/Endings (Lifetime). Looks like a bad ending…. This might not help me personally….

Green: Cauda Drac – Acquisitio – Conjunctio. Endings-Gain-Cooperation. External Judge=Laetitia. Conjunctio has same path and position as in Phoenix Diamond.
Path = Isolation/Cooperation. Time to stop working on this one all by myself…

Purple: Cauda Drac-Conjunctio-Carcer. Endings-Together-Prison? Ending cooperation leads to isolation? Conjunctio has same path and position as in Phoenix Diamond.
Path = Man/Woman (Relationship). Hmm, perhaps advising me/us to not end relationships? Uncertain meaning.

Overall Impression:

Looks like there is a lot to be gained by studying Geomantic Magic Diamonds—But best to do it in cooperation with others, not alone.

Other Observations:

The 8 pathways of the Phoenix Magic Diamond contains four (4) Internal Judges and four(4) External Judges. The Internal Judges are Via, Via, Carcer and Conjunctio. The External Judges are Via, Via, Carcer and Conjunctio—They are a matched set. Significance unknown, but there are two of each in the Fire, and two of each in the Phoenix. Could be that agreement (or lack of it) between the internal and external judges of a reading is significant in some way. Equal numbers, balance, and matching identities is the ground state of the Internal and External Judges in the Phoenix Geomantic Magic Diamond #0105. It feels significant to me, but I don’t know why.

Here are the External Judge paths from the Phoenix Magic Diamond;

Here are the Internal Judge paths;

Yin and Yang

There are six boxes to the left of the vertical row, and six boxes to the right. Five of the six boxes on the right are “negative”, and five of the six boxes on the left are “positive.” If we color them in, it forms a very crude Yin-Yang diagram. Red boxes correspond to the divider of the Yin/Yang Symbol, White and blue are the two colors. There may be other 4X4 diamonds in which the white dot is placed exactly opposite the black dot. Again, it feels significant to me, but the significance unknown.

In the 4X4 diamond there are seven horizontal rows—One box in the top row, two in the second, etc; 1-2-3-4-3-2-1. When you make them into diamonds, Many, but not all, of the other 4X4 Magic Squares exhibit perfect symmetry on all of their 7 rows if you express the numbers in the boxes as 4-digit binary numbers. Be sure to include the leading zeroes—So the number ‘one’ (0001) is symmetrical with the number ‘eight’ (1000) but only if you include the leading zeroes. Significance is unknown.

There are also seven columns in a 4X4 diamond (1-2-3-4-3-2-1). I haven’t even looked at them….

The Internal and External Judges are not a fully developed concept. I had the impression that there WERE Internal and External Judges (see above) but also that they would need to be examined along with some sort of string or line of geomantic figures, perhaps in a circle--but could not find anything on it.

A query on JM Greer’s ‘Magic Mondays’ for April 12th 2020 informed me that there were indeed other folks looking at Geomantic Magic Squares. Thanks, Anonymous, for the link to Digital Ambler--And Thanks to Digital Ambler, whose entire blog is now on my must-read list ;-) !
Following this string of links...

https://ecosophia.dreamwidth.org/85690.html#comments

https://digitalambler.com/2019/02/18/on-geomantic-figure-magic-squares/

https://digitalambler.com/2019/12/09/another-system-of-elemental-affinities-for-the-geomantic-figures/

….Eventually led me to this one:

https://digitalambler.com/2019/12/21/the-chaplet-of-eight-dragons-or-the-rosary-of-the-geomancers-of-allahabad/

The circular “Rosary of the Geomancers of Allahhabad” pictured here feels like the right tool to interpret the significance of the Internal and External Judges. I have no idea how just yet, but when you catch a glimpse of the thing while meditating on the Geo Magic Diamond, and a string of coincidences leads you to a picture from an out-of-print book in French from the 1940’s, well that’s probably the thing you want to look at...

Again, there are 880 different 4X4 Magic Squares. The Phoenix Magic Diamond examined here is only one of them. It could be that selecting the right Magic Diamond is an important part of the Geomantic Diamond reading. It could be that there is only one Diamond that is best for one person’s own use. I have no idea…

Limitations

I am not in any way an expert on Geomancy, Magic Squares, Astrology or generally Occult topics of any kind. If you see something glaringly obvious that I have completely neglected, chances are I just don’t know anything about that. I am pretty certain of the correct placement of the Mothers and Querent-Judge-Quesited-Reconciler groups on the Phoenix Diamond, but not so sure about the Daughters and Nieces.

If you got this far, thanks for reading!
Hopefully this topic was somewhat interesting and even useful. The information seems to be developing like a photograph in a darkroom chemical tray. As more details fill in, I will plan to write about them.

Cheers,

Emmanuel G